SPSS

22.12 Диаграммы нормального распределения

При проведении практически всех статистических тестов важную роль играет вопрос, подчиняются ли анализируемые данные нормальному распределению (для сравнения см. разд. 5.1.2). Проверку нормального распределения можно производить визуально, при помощи гистограммы (для пояснения см. разд. 22.9), однако лучше это осуществлять с использованием специального статистического теста, к примеру, теста Колмогорова-Смирнова (для получения подробной информации см. разд. 14.5). Ещё одну возможность анализа нормального распределения предоставляют диаграммы нормального распределения, которые в SPSS подразделяются на два вида:

•  Р-Р- нормальный вероятностный график

•  Q-Q-нормальный вероятностный график

В первом случае (Р-Р) в форме диаграммы рассеяния на графике отображается зависимость ожидаемых совокупных частот от фактических совокупных частот, а во втором случае (Q-Q) зависимость ожидаемой частоты от наблюдаемой частоты.

Построение диаграмм нормального распределения типа Q-Q можно производить и в рамках предварительного исследования данных. В таком варианте они уже были рассмотрены ранее (для получения подробной информации см. разд. 10.4.1). Поэтому здесь мы приведём пример, касающийся только диаграммы нормального распределения типа Р-Р.

•  Откройте файл hyper.sav и выберите в меню Graphs (Графики) Р-Р... (Р-Р-диаграммы) Откроется диалоговое окно Р-Р Plots (Р-Р-диаграммы).

Рис. 22.62: Диалоговое окно Р-Р Plots (Р-Р-диаграммы)

Вы видите, что тест на нормальное распределение устанавливается по умолчанию. Наряду с этим Вы можете производить тестирование на предмет наличия ещё двенадцати видов распределения, к примеру, на наличие распределения Вайбула (Weibull), Лапласа (Laplace), Хи-квадрат (%2) и /-распределения Стьюдента (Student). Вы можете просмотреть все предлагаемые типы распределений в ниспадающем меню.

•  Мы хотим проверить на предмет нормального распределения переменную а (Alter — возраст); для этого перенесите эту переменную в поле тестируемых переменных.

В диалоговом окне присутствуют также и различные возможности преобразования данных, в состав которых входят: пересчет в натуральные логарифмы, z-преобразование (перевод к стандартизованному виду) и два вида преобразований, применяемых для временных последовательностей.

Для подсчёта ожидаемых значений, подчиняющихся нормальному распределению, на выбор предлагаются четыре различных метода. Если количество значений, полученных в результате наблюдений, обозначить буквой п, а ранговые показатели этих значений буквой г (г = 1, ..., п), то формулы, соответствующие указанным методам, будут выглядеть следующим образом:

Формула Блома (Blom) устанавливается по умолчанию. Далее Вам предоставляется возможность выбора одного из четырёх различных методов для обозначения одинаковых значений (так называемых связок).

•  Оставьте предварительные установки и подтвердите построение диаграммы нажатием ОК.

Будут построены две диаграммы. На первой, простой Р-Р-диаграмме отображается зависимость ожидаемых совокупных частот от фактических совокупных частот, рассчитанная при помощи формулы рангового преобразования Блома (Blom). На второй диаграмме, Р-Р-диаграмме без тренда, отображается разность между фактическими и ожидаемыми совокупными (кумулятивными) частотами в зависимости от фактических совокупных частот.

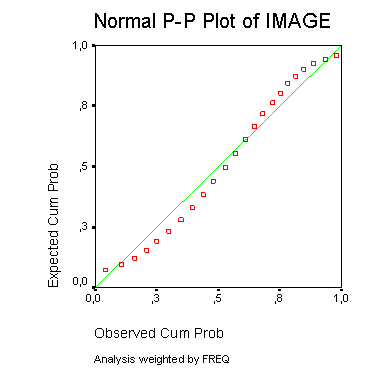
Рис. 22.63: Диаграмма нормального распределения типа Р-Р

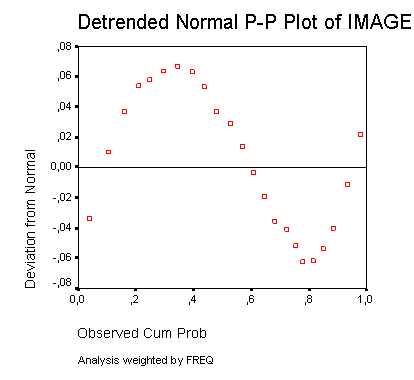
Рис. 22.64: Диаграмма нормального распределения типа Р-Р с исключённым трендом