SPSS

20.5 Кластерный анализ при большом количестве наблюдений (Кластерный анализ методом к-средних)

Иерархические методы объединения, хотя и точны, но трудоёмки: на каждом шаге необходимо выстраивать дистанционную матрицу для всех текущих кластеров. Расчётное время растёт пропорционально третьей степени количества наблюдений, что при наличии нескольких тысяч наблюдений может утомить и серьёзные вычислительные машины.

Поэтому при наличии большого количества наблюдений применяют другие методы. Недостаток этих методов заключается в том, что здесь необходимо заранее задавать количество кластеров, а не так как в иерархическом анализе, получить это в качестве результата Эту проблему можно преодолеть проведением иерархического анализа со случайно отобранной выборкой наблюдений и, таким образом, определить оптимальное количество кластеров. Если количество кластеров указать предварительно, то появляется следующая проблема: определение начальных значений центров кластеров. Их также можно взять из предварительно проведённого иерархического анализа, в котором для каждого наблюдения рассчитывают средние значения переменных, использовавшихся при анализе, а потом в определённой форме сохраняют их в некотором файле. Этот файл может быть затем прочитан методом, который применяется для обработки больших количеств наблюдений. Если нет желания проходить весь этот длинный путь, то можно воспользоваться методом, предлагаемым для данного наблюдения программой SPSS. Если количество кластеров k, которое необходимо получить в результате объединения, задано заранее, то первые k наблюдений, содержащихся в файле, используются как первые кластеры. На последующих шагах кластерный центр заменяется наблюдением, если наименьшее расстояние от него до кластерного центра больше расстояния между двумя ближайшими кластерами. По этому правилу заменяется тот кластерный центр, который находится ближе всего к данному наблюдению. Таким образом получается новый набор исходных кластерных центров. Для завершения шага процедуры рассчитывается новое положение центров кластеров, а наблюдения перераспределяются между кластерами с изменённым центрами. Этот итерационный процесс продолжается до тех пор, пока кластерные центры не перестанут изменять свое положение или пока не будет достигнуто максимальное число итераций.

В качестве примера расчёта по этому алгоритму, рассмотрим выборку из результатов исследований Института социологии Марбургского Университета им. Филипса, в котором проводился опрос 1000 студентов относительно использования ими компьютера и их отношения к современным информационным и телекоммуникационным технологиям. В разделе "Пользование компьютерными программами" были представлены следующие вопросы с различным количеством подпунктов, на которые необходимо было ответить в соответствии с пятибальной шкалой (от отлично до абсолютно не использую): 

1. Насколько свободно вы можете работать в следующих приложениях?

Обработка текста, Графические программы, обработка звука или видео,  монтаж Базы данных и табличные расчёты

2. Насколько хорошо вы владеете следующими языками программирования?

BASIC, Paskal ,С, Машинные языки, Программирование для Интернета(к примеру, HTML), Java 

3. Насколько хорошо Вы можете работать в следующих операционных системах?

DOS , Windows ,UNIX 

4. Насколько хорошо Вы разбираетесь в  следующих возможностях Интернета?

  E-mail, группы новостей,  почтовая рассылка, Путешествие по всемирной сети Интернет, Chat, IRC, ICQ, Предложение собственных услуг(к примеру, домашней страницы)

 5. Насколько хорошо Вы разбираетесь в  играх?

  Как часто Вы играете в компьютерные  игры,  Насколько хорошо Вы ориентируетесь в сценах компьютерных игр?

Ответы на эти вопросы хранятся в переменных vla-v5b в файле computer.sav. В этом файле также находятся и другие переменные, использовавшиеся при исследовании (пол, возраст, место жительства, профессия). На основании вопросов об использовании программных продуктов попытаемся определить группы (кластеры) пользователей. Для начала рекомендуется сократить количество переменных при помощи факторного анализа, как описано в разделе 20.2.3.

•  Откройте файл computer.sav

•  Выберите в меню Analyze (Анализ) Data Reduction (Преобразование данных) Factor... (Факторный анализ)

•  Переменные vla-v5b внесите в список целевых переменных.

•  Через выключатель Extraction... (Отбор) деактивируйте вывод неповёрнутого факторного решения.

•  Через выключатель Rotation... (Вращение) для осуществления вращения активируйте метод варимакса.

•  Минуя выключатель Options... (Опции) в разделе Coefficient Display Format (Формат отображения коэффициентов) (подразумеваются факторные нагрузки) активируйте Sorted by Size (Отсортированные по размеру). Затем активируйте опцию Suppress absolute values less then: (He выводить абсолютные значения меньше чем:) и введите значение ,40.

•  В заключение щёлкните по выключателю Scores... (Значения), чтобы значения факторов сохранить в виде новых переменных.

В результате расчёта было отобрано четыре фактора и добавлено в файл четыре переменные от (fac1_1 до fac4_1), которые и отображают эти четыре фактора. Среди результатов присутствует повёрнутая факторная матрица (см. следующую таблицу).

Факторная матрица красноречиво демонстрирует, что отобранные факторы могут быть расположены в следующей смысловой последовательности (по убыванию значимости):

•  Приложение

•  Программирование

•  Использование Интернета

•  Игры

Rotated Component Matrix

(Повёрнутая матрица компонентов)
	Component (Компонент)
	1	2	3	4
Textverarbeitung (Обработка текста)	,848
Windows	,840
DOS	,653
WWW	,619
Datenbanken (Базы данных и табличные расчёты)	,611
Multimedia (Мультимедиа)	,535
С		,771
Maschinensprache (Машинные языки)		,741
PASCAL		,729
BASIC		,612
Java		,606	,474
UNIX		,587	,504
Chat			,699
eigene Dienste (Предложение собственных услуг )			,696
Internetsprachen (Программирование для Интернет)		,468	,670
Email	,584		,609
ICQ			,601
Szene (Сцены компьютерных игр)				,881
Intensitaet (Интенсивность)				,850

Extraction Method: Principal Component Analysis (Метод отбора: Анализ главных компонентов).

Rotation Method: Varimax with Kaiser Normalization (Метод вращения: варимакс с нормализацией Кайзера).

a. Rotation converged in 11 iterations (Вращение осуществлено за 11 итераций).

Теперь используем сохранённые нами значения этих четырёх факторов для проведения кластерного анализа для студентов. Так как количество наблюдений равное 1085 слишком велико для иерархического кластерного анализа, выберем метод анализа кластерных центров.

•  Присвойте переменным fac1_1-fac4_1 метки: "Приложения", "Программирование", "Использование Интернет" и "Игры" соответственно.

•  Выберите в меню Analyze (Анализ) Classify (Классифицировать) K-Means Cluster... (Кластерный анализ методом к-средних)

Откроется диалоговое окно K-Means Cluster Analysis (Кластерный анализ методом к-средних).

Рис. 20.4: Диалоговое окно K-Means Cluster Analysis (Анализ кластерных центров)

•  Переменные от fac1_1 до fac4_1 поместите в поле тестируемых переменных. Теперь Вы подошли к тому месту, где нужно указывать количество кластеров. Подходящим вариантом было бы сперва провести иерархический кластерный анализ для произвольно выбранных наблюдений и получившееся количество кластеров принять за оптимальное. Вы, конечно же, можете провести и несколько опытных, пробных расчётов с различным количеством кластеров и после этого определиться с подходящим вариантом решения.

•  Мы остановимся на четырёх кластерах; введите это значение в поле Number of Clusters (Количество кластеров).

•  Через выключатель Iterate... (Итерации) укажите число итераций равное 99; установленное по умолчанию количество итераций равное 10, оказалось бы недостаточным.

•  Щёлкните по выключателю Save... (Сохранить), чтобы при помощи дополнительных переменных зафиксировать принадлежность наблюдений к кластеру.

•  Щёлкните на ОК, чтобы начать расчёт.

Сначала приводятся первичные кластерные центры и обобщённые данные итерационного процесса (30 итераций); затем выводятся окончательные кластерные центры и информация о количестве наблюдений.

Final Cluster Centers 

(Кластерные центры окончательного решения)
	Cluster (Кластер)
	1	2	3	4
Приложение	-,15219	-,62362	-,23459	1,16856
Программирование	-2,91321	,232223	,23371	,05918
Использование Интернет	-1,71057	,7232	-.02994	,25268
Игры	,04717	,51053	-1,51014	,26081

При оценке кластерных центров следует в первую очередь обратить внимание на то, что здесь речь идёт о средних значениях факторов, которые находятся в пределах примерно от -3 до +3. К тому же, надо помнить, что в соответствии с кодировкой ответов (1 = отлично, 5 = абсолютно не использую) большое отрицательное значение фактора означает его большую степень его проявления, то есть сигнализирует о высокой компетентности, и наоборот, большое положительное значение фактора подразумевает низкую степень его проявления.

Если учесть всё вышесказанное, то наши четыре кластера можно интерпретировать следующим образом:

Кластер1: Программисты, Интернет-эксперты

Кластер2: Пользователи стандартного программного обеспечения

КластерЗ: Игроки

Кластер4: Начинающие пользователи

В заключение выводятся показатели количества наблюдений, относящихся к каждому из кластеров. Группа пользователей (кластер 2) наиболее многочисленна.

Number of Cases in each Cluster 

(Количество наблюдений в каждом кластере)
Cluster (Кластер)	1	63,000
	2	488,000
	3	221,000
	4	313,000
Valid (Действительные)		1085,000
Missing (Отсутствующие)		,000

К исходному файлу была добавлена переменная qc1_1, отражающая принадлежность к определённому кластеру. Эту переменную можно использовать для обнаружения возможных связей между кластерной принадлежностью и полом, возрастом, профессией и происхождением (западные земли Германии, восточные земли Германии, зарубежные страны).

Наряду с количеством кластеров можно так же, как было упомянуто в начале главы, задать и первичные кластерные центры. Для этого их необходимо определённым образом ввести в файл данных SPSS. Изучим процесс создания такого файла на рассмотренном примере,

•  После щёлка в диалоговом окне K-Means Cluster Analysis (Кластерный анализ методом k-средних) по выключателю Centers» (Центры), диалоговое окно примет расширенный вид (см. рис. 20.5).

•  Активируйте Read initial from (Читать первичные значения из) и щёлкните на выключателе File... (Файл). Откроется диалоговое окно K-Means Cluster Analysis: Read initial from (Кластерный анализ методом К-средних: Читать первичные значения из).

•  Откройте файл zentren.sav.

Файл содержит

•  количественную переменную с именем cluster_

•  одну строку для каждого кластера

•  первичные значения для каждой кластерной переменной.

То, как выглядит этот файл в редакторе данных, Вы можете увидеть на рисунке 20.6. Аналогично тому, как Вы смогли считать из файла первичные кластерные центры, при помощи выключателя Write final as (Сохранить окончательные результаты как), Вы можете сохранить окончательные кластерные центры в отдельном файле для дальнейших расчётов.

Рис. 20.5: Диалоговое окно K-Means Cluster Analysis (Анализ кластерных центров)

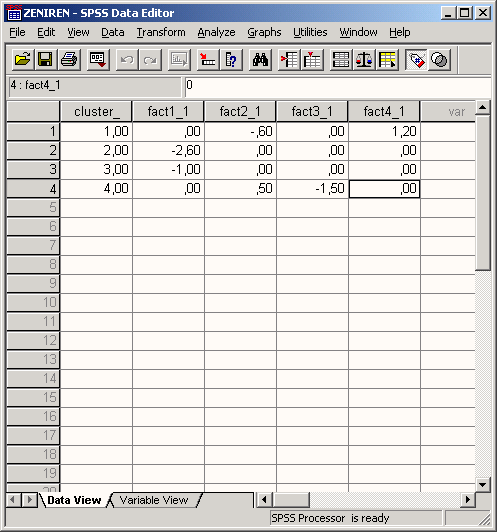
Рис. 20.6: Файл с первичными кластерными центрами

Мы надеемся, что при помощи приведенных примеров нам удалось пробудить у Вас интерес к кластерному анализу и облегчить понимание интереснейших статистических методов.