SPSS

15.3 Частная корреляция

Если исследовать достаточно большую совокупность мужчин и сопоставить размер их обуви с уровнем образованности, то между этими двумя переменными можно заметить хоть и небольшую, но в то же время значимую корреляцию. Это корреляция может послужить примером так называемой ложной корреляции. Здесь статистически значимый коэффициент корреляции является не проявлением некоторой причинной связи между двумя рассматриваемыми переменными, а в большей степени обусловлен некоторой третьей переменной.

В рассматриваемом примере такой переменной является рост. С одной стороны существует некоторая незначительная корреляция между ростом и уровнем образованности, а с другой — вполне объяснимая и логичная связь между ростом и размером обуви. Вместе эти две корреляции приводят к упоминавшейся ложной корреляции. Для исключения одной такой искажающей переменной необходим расчёт так называемой частной корреляции.

Если присвоить коррелирующим переменным индексы 1 и 2, а искажающей переменной — индекс 3, и попарно рассчитать корреляционный коэффициент (Пирсона) r₁₂,r₁₃, и r₂₃ , то для частных корреляционных коэффициентов получим:

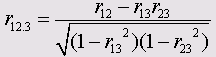
Достаточно давно в социологических исследованиях, проводимых в Германии, выяснялось отношение населения к приезжим рабочим-иностранцам. Для этого было сформулировано несколько отдельных вопросов. Ответы на вопросы суммировались. Сумма могла принимать значения от 0 до 30, причём большее значение соответствует более негативному отношению к приезжим рабочим.

Среди многочисленных дополнительных переменных учитывались: возраст опрашиваемых и частота посещения церкви. Последней характеристике были присвоены значения от 1 (никогда) до 6 (по меньшей мере, 2 раза в неделю). Небольшая выборка из оригинальных данных опроса (35 респондентов с этими тремя переменными) наводится в файле kirche.sav. Откройте этот файл, если Вы хотите самостоятельно провести следующие расчёты.

Если подсчитать корреляции между этими тремя переменными, то при выборе коэффициентов Пирсона для анализа взаимосвязи, получатся следующие результаты закроем глаза на то, что одна из переменных, а именно частота посещения церкви, имеет порядковую шкалу):

Correlations (Корреляции)

"* Correlation is significant at the .01 level (2-tailed). Корреляция является закономерной на уровне 0,01 (2-стороння).

Принимая во внимание полярность, полученные результаты можно трактовать, к примеру, таким образом, что частые посещения церкви коррелируют с отрицательным отношением к приезжим рабочим (r = 0,432). Прежде, чем поставить в упрёк церкви враждебность по отношению к иностранцам, нужно учесть влияние возраста. Он также коррелирует с враждебным отношением к иностранным рабочим (r = 0,468) и сильно коррелирует с частотой посещения церкви (r = 0.779). Таким образом, возникает подозрение, что возраст является искажающим признаком, виновным в ложной корреляции между частотой посещения церкви и отрицательным отношением к иностранным рабочим. Докажем это путём расчёта частных корреляционных коэффициентов.

•  Откройте файл kirche.sav.

•  Выберите в меню Analyse... (Анализ) Correlate... (Корреляция) Partial... (Частная)

Откроется диалоговое окно Partial Correlations (Частные корреляции).

•  Перенесите переменные gast и kirche в поле признаков, а переменную alter в поле контрольных переменных и оставьте предварительную установку для двухстороннего теста значимости.

При помощи щелчка на кнопке Options... (Опции) наряду с традиционной обработкой пропущенных значений, Вы можете организовать расчёт среднего значения, стандартного отклонения и вывод «корреляций нулевого порядка» (то есть простых корреляционных коэффициентов).

В случае одной искажающей переменной, как в приведенном примере, возможен расчёт частной корреляции первого порядка, при наличии нескольких искажающих переменных, SPSS выдаёт корреляции высших порядков.

•  Начните расчёт щелчком на кнопке ОК. Вязкие просмотра появится следующий результат:

Вас, возможно, удивит, что в данном случае всё ещё выводится старый вариант таблицы результатов, соответствующий прежним версиям SPSS. Результаты включают: частный корреляционный коэффициент, число степеней свободы (число наблюдений минус 3) и уровень значимости. Исходя из полученных результатов, можно сделать вывод, что при исключении искажающей переменной alter больше не наблюдается существенной корреляции между частотой посещения церкви и отрицательным отношением к иностранным рабочим.

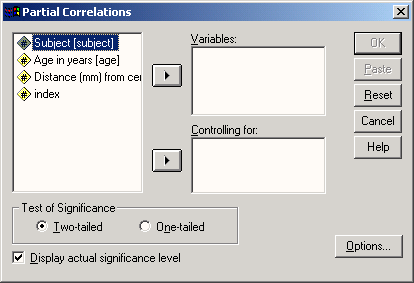
Рис. 15.3: Диалоговое окно Partial Correlations (Частичные корреляции)