SPSS
обработка статистической информации
 |
 |
 |
14.7 Биномиальный тест
Этот тест проверяет дихотомические переменные на наличие различия между частотами обоих проявлений признака. Недихотомические переменные могут быть диэтомизированы (разделены на две категории) при помощи задания некоторой разделительной величины.
Представьте себе, что Вы играете со своим партнёром по теннису 50 матчей и выигрываете 29. Ваш партнёр, выигравший 21 раз, думает, что Вы ничем не лучше, а эта разница является случайной.
Чтобы это проверить можно выполнить биномиальный тест.
-
Откройте файл match.sav, содержащий две переменные: spieler и n.
Первая переменная имеет кодировки 1 и 2, которые соответствуют двум игрокам. Переменная n указывает на частоту выигрыша; ей присваивается статус весовой переменной.
-
Сначала выберите в меню Data (Данные) Weight Cases (Взвесить наблюдения)
-
Укажите переменную п как частотную переменную (см. гл. 8.7).
-
Затем выберите в меню Analyze (Анализ) Nonparametric Tests (Непараметрические тесты) Binomial (Биномиальное распределение)
Откроется диалоговое окно Binomial Test (Тест на биномиальное распределение) см. рис. 14. 7.
-
Перенесите щелчком переменную spieler в поле тестируемых переменных.
Если бы эта переменная не была дихотомической, Вы бы могли в поле Определить дихотомию (Define Dichotomy) ввести разделительную величину для проведения раздвоения (дихотомизации). Предварительно установленная тестовая пропорция (0,50) показывает на ожидаемую относительную частоту появления первой из двух дихотомических категорий. Здесь Вы можете задать и другое значение. После нажатия кнопки Options... (Опции) Вы можете организовать вывод (абсолютно бессмысленных) характеристик дескриптивной статистики.
-
Запустите расчёт путём нажатия ОК.
В окне просмотра появятся следующие результаты:
Binomial Test (Тест на биномиальное распределение)
| Category (Категория) |
N |
Observed Prop. (Наблюда- емая пропорция) |
Test Prop. (Тестовая пропорция) |
Asymp. Sig. (2-tailed) (Статисти- ческая значимость (2-сторонняя)) |
||
| SPIELER (Игрок) |
Группа 1 |
1 |
29 |
,58 |
,50 |
,322а |
| Группа 2 |
2 |
21 |
,42 |
|
|
|
| Total (Сумма) |
|
50 |
1,00 |
|
|
|
a. Based on Z Approximation. (Основываясь на Z-аппроксимации.)
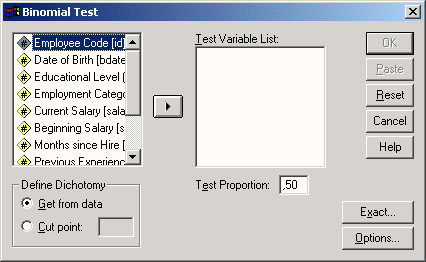
Рис. 14.7: Диалоговое окно Тест на биномиальное распределение
В выводимые результаты включают наблюдаемые абсолютные и относительные частоты обеих категорий, а так же ожидаемую относительную частоту первой категории Полученная вероятность ошибки (р = 0,322) говорит о том, что между наблюдаемой и ожидаемой относительными частотами не существует значимого различия. Стало быть и разница между обеими частотами выигрыша не является значимой.
 |
 |
 |
Новости
Информация
Улица Новомосковская 36
500003 Екатеринбург
E-mail: inform@