SPSS

11.3.1 Тест хи-квадрат (X²)

При проведении теста хи-квадрат проверяется взаимная независимость двух переменных таблицы сопряженности и благодаря этому косвенно выясняется зависимость обоих переменных. Две переменные считаются взаимно независимыми, если наблюдаемые частоты (f₀) в ячейках совпадают с ожидаемыми частотами (f_e).

Для того, чтобы провести тест хи-квадрат с помощью SPSS, выполните следующие действия:

•  Выберите в меню команды Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Crosstabs... (Таблицы сопряженности)

•  Кнопкой Reset (Сброс) удалите возможные настройки.

•  Перенесите переменную sex в список строк, а переменную psyche — в список столбцов.

•  Щелкните на кнопке Cells... (Ячейки). В диалоговом окне установите, кроме предлагаемого по умолчанию флажка Observed, еще флажки Expected и Standardized. Подтвердите выбор кнопкой Continue.

•  Щелкните на кнопке Statistics... (Статистика).

Откроется описанное выше диалоговое окно Crosstabs: Statistics.

•  Установите флажок Chi-square (Хи-квадрат). Щелкните на кнопке Continue, а в главном диалоговом окне — на ОК.

Вы получите следующую таблицу сопряженности.

Пол * Психическое состояние Таблица сопряженности

				Психическое состояние			Total
			Крайне неустой-чивое	Неустой-чивое	Устой-чивое	Очень устойчивое
Пол	женский	Count	16	18	9	1	44
		Expected Count	7,9	16,6	17,0	2,5	44,0
		Std. Residual	2,9	,3	-1,9	-.9
	Мужской	Count	3	22	32	5	62
		Expected Count	11,1	23,4	24,0	3,5	62,0
		Std. Residual	-2,4	-,3	1,6	,8
Total		Count	19	40	41	6	106
		Expected Count	19,0	40,0	41,0	6,0	106,0

Кроме того, в окне просмотра будут показаны результаты теста хи-квадрат: 

Chi-Square Tests (Тесты хи-квадрат)

	Value (Значение)	df	Asymp. Sig. (2-sided) (Асимптотическая значимость (двусторонняя))
Pearson Chi-Square (Хи-квадрат по Пирсону)	22,455 (а)	3	,000
Likelihood Ratio (Отношение правдоподобия)	23,688	3	,000
Linear-by-Linear Association (Зависимость линейный-линейный)	20,391	1	,000
N of Valid Cases (Кол-во допустимых случаев)	106

а. 2 cells (25,0%) have expected count less than 5. The minimum expected count is 2,49 (2 ячейки (25%) имеют ожидаемую частоту менее 5. Минимальная ожидаемая частота 2,49.)

Для вычисления критерия хи-квадрат применяются три различных подхода: формула Пирсона, поправка на правдоподобие и тест Мантеля-Хэнзеля. Если таблица сопряженности имеет четыре поля и ожидаемая вероятность менее 5, дополнительно выполняется точный тест Фишера.

Критерий хи-квадрат по Пирсону

Обычно для вычисления критерия хи-квадрат используется формула Пирсона:

Здесь вычисляется сумма квадратов стандартизованных остатков по всем полям таблицы сопряженности. Поэтому поля с более высоким стандартизованным остатком вносят более весомый вклад в численное значение критерия хи-квадрат и, следовательно, — в значимый результат. Согласно правилу, приведенному в разделе 8.7.2, стандартизованный остаток 2 или более указывает на значимое расхождение между наблюдаемой и ожидаемой частотами.

В рассматриваемом нами примере формула Пирсона дает максимально значимую величину критерия хи-квадрат (р<0,001). Если рассмотреть стандартизованные остатки в отдельных полях таблицы сопряженности, то на основе вышеприведенного правила можно сделать вывод, что эта значимость в основном определяется полями, в которых переменная psyche имеет значение "крайне неустойчивое". У женщин это значение сильно повышено, а у мужчин — понижено.

Корректность проведения теста хи-квадрат определяется двумя условиями: во-первых, ожидаемые частоты < 5 должны встречаться не более чем в 20 % полей таблицы; во-вторых, суммы по строкам и столбцам всегда должны быть больше нуля.

Однако в рассматриваемом примере это условие выполняется не полностью. Как указывает примечание после таблицы теста хи-квадрат, 25 % полей имеют ожидаемую частоту менее 5. Однако, так как допустимый предел4в 20 % превышен лишь ненамного и эти поля, вследствие своего очень малого стандартизованного остатка, вносят весьма незначительную долю в величину критерия хи-квадрат, это нарушение можно считать несущественным.

Критерий хи-квадрат с поправкой на правдоподобие

Альтернативой формуле Пирсона для вычисления критерия хи-квадрат является поправка на правдоподобие:

При большом объеме выборки формула Пирсона и подправленная формула дают очень близкие результаты. В нашем примере критерий хи-квадрат с поправкой на правдоподобие составляет 23,688.

Тест Мантеля-Хэнзеля

Дополнительно в таблице сопряженности под обозначением linear-by-linear ("линейный-по-линейному") выводится значение теста Мантеля-Хэнзеля (20,391). Эта форма критерия хи-квадрат с поправкой Мантеля-Хэнзеля — еще одна мера линейной зависимости между строками и столбцами таблицы сопряженности. Она определяется как произведение коэффициента корреляции Пирсона на количество наблюдений, уменьшенное на единицу:

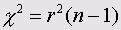
Полученный таким образом критерий имеет одну степень свободы. Метод Мантеля-Хэнзеля используется всегда, когда в диалоговом окне Crosstabs: Statistics установлен флажок Chi-square. Однако для данных, относящихся к с номинальной шкале, этот критерий неприменим.