SPSS

10.4.1 Анализ без группирующей переменной

Проведем анализ возраста пациентов.

•  Перенесите переменную а в список зависимых переменных (Dependent List). Так как сначала мы хотим выяснить, какие методы анализа выполняются по умолчанию, то не будем пока вносить никаких изменений в настройки.

•  Запустите вычисление, щелкнув на кнопке ОК. Будут созданы следующие таблицы:

Case Processing Summary (Обработанные наблюдения)

	Cases (Случаи)
	Valid (Допустимые)		Missing (Отсутствующие)	Total (Всего)
N	Percent	N Percent	N	Percent
Возраст	174	100,0%	0 ,0%	174	100,0%

Descriptives (Описательная статистика)

			Statistic	Std. Error
Возраст	Mean (Среднее)		62,11	,88
	95% Confidence Interval for Mean (95% доверительный интервал среднего)	Lower Bound (Нижняя граница) Upper Bound (Верхняя граница)		60,38 63,84
	5% Trimmed Mean (5% усеченное среднее)		62,25
	Median (Медиана)		63,00
	Variance (Дисперсия)		133,358
	Std. Deviation (Стандартное отклонение)		11,55
	Minimum (Минимум)		36
	Maximum (Максимум)		87
	Range (Размах)		51
	Interquartile Range (Межквартильная широта)		17,25
	Skewness (Асимметрия)		-,143	,184
	Kurtosis (Коэффициент вариации)		-,635	,366

Возраст Stem-and-Leaf Plot (диаграмма ветвей и листьев)

Frequency	Stem &	Leaf
6,00	3 .	677999
7,00	4 .	0223333
14,00	4 .	66677788888999
23,00	5 .	01111111122223333333444
20,00	5 .	55667777778888888899
27,00	6 .	000011111222333333333444444
27,00	6 .	555555666666677888888999999
24,00	7 .	000000011111122233333444
13,00	7 .	5566666788899
11,00	8 .	00001111224
2,00	8 .	67
Stem width :	10
Each leaf:		1 case(s)

В этом случае окно вывода результатов содержит:

•  статистические характеристики,

•  диаграмму stem-and-leaf (ветвей и листьев)

•  коробчатую диаграмму (box plot).

Большую часть статистических характеристик мы уже рассмотрели в главах 6 и 9. Появились новые характеристики:

•  5% усеченное среднее: среднее значение, вычисленное без учета 5% наименьших и 5% наибольших значений.

•  95% доверительный интервал: доверительный интервал, в котором находится среднее значение с вероятностью 95%.

•  Межквартилъная широта: расстояние между первым и третьим квартилями.

Диаграмма ветвей и листьев представляет собой комбинацию гистограммы и табличного списка. Как на гистограмме, длина каждой строки соответствует количеству наблюдений, попадающих в определенный интервал. Но, сверх этого, на данной диаграмме выводится также наблюдаемое численное значение для каждого наблюдения. Для этой цели численное значения разбиваются на два компонента: ветвь, представляющую собой первую цифру или группу цифр и лист — последующие цифры. Ветвь соответствует тем разрядам численного значения наблюдаемой переменной, которые не изменяются, а листья — разрядам, которые изменяются в пределах избранного интервала. В рассматриваемом примере ветви разбиты на две части — одну для листьев с 0 по 4 и другую — для листьев с 5 по 9.

Коробчатая диаграмма состоит из прямоугольника, занимающего пространство от первого до третьего квартиля (то есть, от 25 до 75 процентиля). Линия внутри этого прямоугольника соответствует медиане. Кроме того, на коробчатой диаграмме отмечаются максимальное и минимальное значения, если только они не являются выбросами (см. ниже).

Значения, удаленные от границ более чем на три длины построенного прямоугольника (экстремальные значения), помечаются на диаграмме звездочками. Значения, удаленные более чем на полторы длины прямоугольника, помечаются кружками.

Теперь посмотрим, какие еще статистические характеристики можно вычислить в дополнение к стандартным.

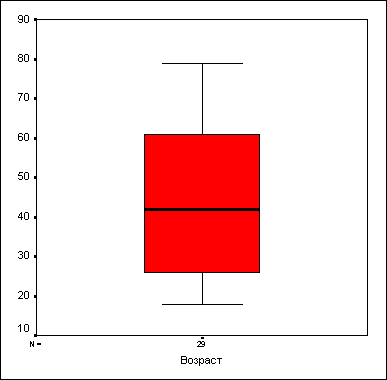
Рис. 10.2: Коробчатая диаграмма

•  В диалоговом окне Explore щелкните на кнопке Statistics... (Статистика).

Откроется диалоговое окно Explore: Statistics (см. рис. 10.3).

•  Статистические характеристики, установленные по умолчанию уже вычислены, поэтому флажок для них (Descriptives) можно снять.

•  Установите флажки для вычисления М-оценок Губера, Тьюки, Эндрюса и Хампеля (М-estimators), выбросов (Outliers) и процентилей (Percentiles).

•  Закройте диалог, щелкнув на Continue, и запустите вычисления кнопкой ОК. Результат этих вычислений приводится ниже.

 

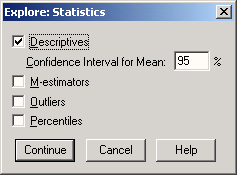
Рис. 10.3: Диалоговое окно Explore: Statistics

M-Estimators

	Huber's M-Estimator ia) (М-оценка Губера)	Tukey's Biweight (b) (Оценка Тьюки)	Hampel M-Estimator (с) (М-оценка Хампеля)	Andrews' Wave (d) (Волна Эндрюса)
Возраст	62,38	62,51	62,31	62,51

a. The weighting constant is 1,339 (Весовая константа равна 1,339).

b. The weighting constant is 4,685 (Весовая константа равна 4,685).

с. The weighting constants are 1,700, 3,400 and 8,500 (Весовые константы равны 1,700, 3,400 и 8,500).

d. The weighting constant is 1,340*pi (Весовая константа равна 1,340*pi).

Percentiles

	Percentiles
	5	10	25	50	75	90	95
Weighted Возраст Average(Definition 1 ) (Взвешенное среднее, определение 1 )	42,00	47,00	53,00	63,00	70,25	78,00	81,00
Tukey's Hinges Возраст (угловые точки Тьюки)			53,00	63,00	70,00

Extreme Values (Экстремальные значения)

			Case Number (Номер случая)	Value (Значение)
Возраст	Highest (Наибольшие значения)	1	96	87
		2	53	86
		3	99	84
		4	86	82
		5	62	82
	Lowest (Наименьшие значения)	1	68	36
		2	23	37
		3	64	37
		4	122	39
		5	45	.а

a. Only a partial list of cases with the value 39 are shown in the table of lower extremes (В таблице наименьших экстремальных значений показан только частичный список наблюдений со значением 39).

В этих таблицах выводятся М-оценки Губера, Тьюки, Хампеля и волна Эндрюса. Основная идея М-оценок состоит в том, чтобы перед вычислением среднего значения присвоить отдельным наблюдениям разные веса. В распространенных М-оценках применяются веса, уменьшающиеся с удалением от центра распределения. Следовательно, обычное среднее значение можно рассматривать как М-оценку с единичными весами для всех наблюдений.

Из возможных процентилей выводятся семь значений: для 5, 10, 25, 50, 75, 90 и 95 процентов. Дополнительно вычисляются угловые точки Тьюки: 25%, 50% и 75%-про-центили.

В таблице «Экстремальные значения» выводятся пять наибольших и пять наименьших значений (выбросы).

Теперь обратимся к диаграммам, которые можно построить при исследовании данных в SPSS.

•  В диалоговом окне Explore щелкните на кнопке Plots... (Диаграммы). Откроется диалоговое окно Explore: Plots (см. рис. 10.4).

С коробчатой диаграммой и диаграммой ветвей и листьев мы уже ознакомились.

•  Поэтому в поле Boxplots (Коробчатые диаграммы) выберите опцию None (Нет) и снимите флажок Stem-and-leaf; вместо него установите флажок Histogram (Гистограмма).

•  Щелкните на кнопке Continue, а затем на ОК. В окне просмотра появится гистограмма.

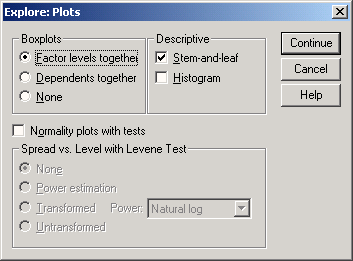
Рис. 10.4: Диалоговое окно Explore: Plots

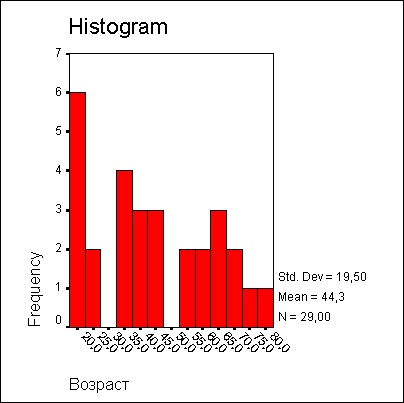
Рис. 10.5: Гистограмма возрастной структуры

Далее мы посмотрим, какие результаты можно получить, если установить в диалоговом окне Explore: Plots флажок Normality plots with tests (Диаграмма нормального распределения с тестами).

•  Установите этот флажок и подтвердите настройку кнопкой ОК.

В окне просмотра будет показан результат теста Лиллифора (модификации теста Колмогорова-Смирнова) на нормальное распределение.

Если в результате получена вероятность ошибки р менее 0,05, то данное распределение значимо отличается от нормального. В данном примере при р = 0,200 распределение можно считать нормальным. При объеме выборки менее 50 наблюдений проводится также тест Шапиро-Уилкса.

Tests of Normality (Тесты на нормальное распределение)

	Kolmoqorov-Smirnov (а) (Колмогоров-Смирнов)
Statistic	df	Sig.
Возраст	,059	174	,200*

*. This is a lower bound of the true significance (Это нижняя граница истинной значимости), a. Lilliefors Significance Correction (Коррекция значимости по Лиллифору).

В окне просмотра будут показаны две диаграммы:

•  диаграмма нормального распределения

•  диаграмма с исключенным трендом

По диаграмме нормального распределения (также называемой диаграммой Q-Q) можно визуально определить, достаточно ли близко заданное распределение приближается к нормальному. Здесь каждое наблюдаемое значение сравнивается со значением, ожидаемым при нормальном распределении. При условии точного выполнения нормального распределения все точки лежат на прямой. Наблюдаемые значения откладываются по оси X, а ожидаемые — по оси Y, при этом все значения подвергаются стандартизации (z-преобразованию). В данном примере (см. рис. 10.6) наблюдаемые значения достаточно близки к прямой.

Рис. 10.6: Диаграмма нормального распределения

На диаграмме с исключенным трендом отклонения наблюдаемых значений от ожидаемых при нормальном распределении представлены в зависимости от наблюдаемых значений. В случае нормального распределения все точки лежат на горизонтальной прямой, проходящей через нуль. Явное отклонение от прямой указывает на отличие распределения от нормального. На этой диаграмме все значения, также подвергаются стандартизации (z-преобразованию) (см. рис. 10.7).

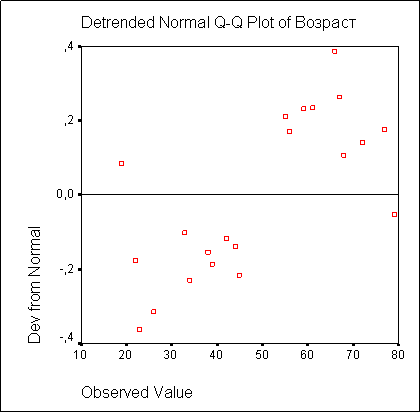
Рис. 10.7: Диаграмма с исключенным трендом

Заканчивая рассмотрение диалога Explore... (Исследовать), следует упомянуть еще кнопку Options... (Параметры), которая позволяет задать способ обработки пропущенных значений, и содержит группу опций Display (Показывать). Последняя позволяет запретить вывод диаграмм или статистических таблиц.